RSA算法

# RSA 加密

$$密文 = 明文^E mod N$$

E 为 encryption (加密) 的缩写

# RSA 解密

$$明文 = 密文^D mod N$$

D 为 decryption (解密) 的缩写

# 生成密钥对

密钥对为（E, D, N）

要生成密钥对，还要分别求出 N, L, E, D

# 求 N

$$N = p × q$$

其中 p 和 q 是两个质数（素数），这两个质数不能太小，否则容易被破解

质数又称素数，一个大于 1 的自然数，除了 1 和它自身外，不能被其他自然数整除的数叫做质数

# 求 L

$$L = (p-1) × (q-1)$$

$$L = lcm(p-1, q-1)$$

其中 L 是 p-1 和 q-1 的最小公倍数，lcm 就是最小公倍数的意思

L 是一个中间变量，我们需要求出 L 以求出 E

# 求 E

$$1<E<L$$

$$gcd(E, L) = 1$$

E 是一个比 1 大但是比 L 即 lcm 小的数，gcd 就是最大公约数的意思

# 求 D

$$1<D<L$$

$$E × D mod L = 1$$

# 实战：

了解了原理之后我们来实战一下

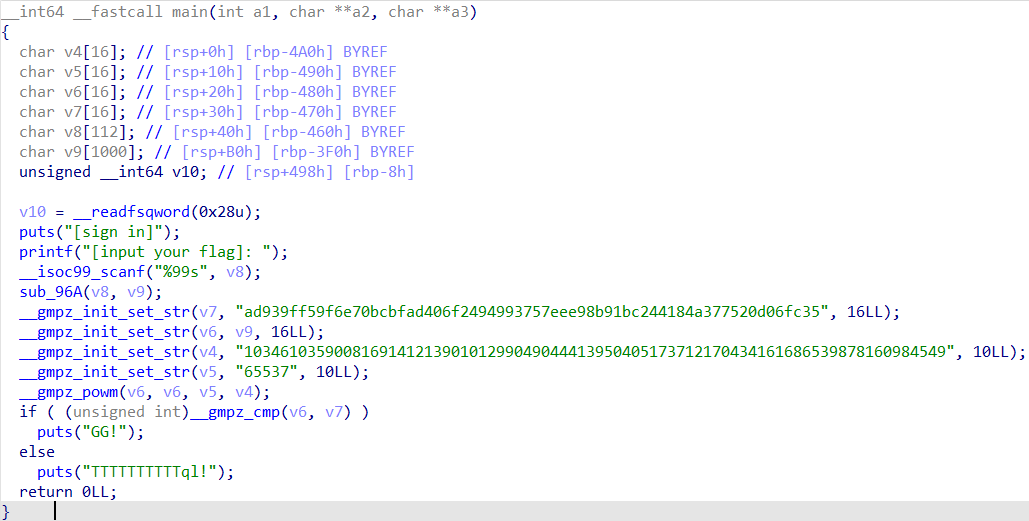
这有一道题

很明显，其中 E 指数 = 65537，N = 103461035900816914121390101299049044413950405173712170434161686539878160984549

而 ad939ff59f6e70bcbfad406f2494993757eee98b91bc244184a377520d06fc35 则是 16 进制密文

我们可以通过分解 N 来求 p 和 q，可以用 http://www.factordb.com/ 这个网站来分解，分解得到

1
2

p = 282164587459512124844245113950593348271
q = 366669102002966856876605669837014229419

这样我们就可以通过 p-1 和 q-1 来求 L ，但 L 只是一个中间变量，我们现在可以不求出来，最后用脚本代入即可，求出 L 之后就可以求出 D，求出 D 之后就可以解出来了

$$明文 = 密文^D mod N$$

# 脚本如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14

import gmpy2
import binascii

p = 282164587459512124844245113950593348271
q = 366669102002966856876605669837014229419
E = 65537
miwen = 0xad939ff59f6e70bcbfad406f2494993757eee98b91bc244184a377520d06fc35

N = p * q
D = gmpy2.invert(E, (p-1) * (q-1))
mingwen = gmpy2.powmod(miwen, D, N)

print(binascii.unhexlify(hex(mingwen)[2:]).decode(encoding="utf-8"))

解出 flag 为：suctf{Pwn_@_hundred_years}

题目来源：BUUCTF 在线评测 (buuoj.cn)

参考博客：(25 条消息) 带你彻底理解 RSA 算法原理_小宝一号的博客 - CSDN 博客_rsa 是哪个国家